改进随机森林的第二部分
我们已经构建了一个随机森林模型来解决我们的机器学习问题（也许是通过遵循这个端到端指南），但我们对结果并不太满意。我们有哪些选择？正如我们在这个系列的第一部分中看到的那样，我们的第一步应该是收集更多数据并进行特征工程。收集更多数据和进行特征工程通常在时间投入与性能改善之间具有最大的回报，但当我们已经耗尽了所有数据来源时，就是时候转向模型超参数调整了。本文将重点介绍使用Scikit-Learn工具优化Python中的随机森林模型。虽然本文是在第一部分的基础上构建的，但它完全独立存在，并且我们将涵盖许多广泛适用的机器学习概念。
随机森林中的一棵树
我在本文中包含了Python代码，以便在最有教育意义的地方进行演示。可以在项目Github页面上找到完整的代码和数据。
超参数调整的简要说明
最好的方法是将超参数视为可以调整以优化性能的算法设置，就像我们可能会调整AM收音机的旋钮以获得清晰的信号（或者你的父母可能会这样做！）。虽然模型参数是在训练期间学习的，比如线性回归中的斜率和截距，但超参数必须在训练之前由数据科学家设置。在随机森林的情况下，超参数包括森林中的决策树数量以及每个树在分裂节点时考虑的特征数量（随机森林的参数是用于分裂每个节点的变量和阈值，在训练期间学习）。Scikit-Learn为所有模型实现了一组明智的默认超参数，但这些不能保证在解决问题时是最优的。最佳超参数通常是不可能提前确定的，而调整模型是机器学习从科学转变为基于试错的工程的地方。
超参数调整更多地依赖于实验结果而不是理论，因此确定最佳设置的最佳方法是尝试许多不同的组合并评估每个模型的性能。然而，仅在训练集上评估每个模型可能会导致机器学习中最基本的问题之一：过拟合。
如果我们为训练数据优化模型，那么我们的模型在训练集上得分非常高，但无法推广到新数据，例如测试集。当模型在训练集上表现良好但在测试集上表现不佳时，这被称为过拟合，或者基本上是创建了一个非常熟悉训练集但无法应用于新问题的模型。这就像一个已经记住了教科书中简单问题的学生，但不知道如何在杂乱的现实世界中应用概念。
过度拟合的模型在训练集上看起来令人印象深刻，但在实际应用中将是无用的。因此，超参数优化的标准程序通过交叉验证来解决过拟合问题。
交叉验证
交叉验证（CV）技术最好通过使用最常见的方法之一——K折交叉验证进行说明。当我们解决机器学习问题时，我们确保将数据拆分为训练集和测试集。在K折交叉验证中，我们将训练集进一步拆分为K个子集，称为折叠。然后，我们进行K次迭代，每次将数据训练在K-1个折叠上，并在第K个折叠上进行评估（称为验证数据）。例如，考虑使用K = 5拟合模型。第一次迭代，我们在前四个折叠上进行训练，并在第五个折叠上进行评估。第二次我们在第一、第二、第三和第五个折叠上进行训练，并在第四个折叠上进行评估。我们重复此过程3次，每次在不同的折叠上进行评估。在训练结束时，我们平均每个折叠的性能，得出模型的最终验证指标。
对于超参数调整，我们执行许多整个K-Fold CV过程的迭代，每次使用不同的模型设置。然后我们比较所有模型，选择最好的模型，在完整的训练集上进行训练，然后在测试集上进行评估。这听起来非常繁琐！每次我们想评估不同的超参数集时，我们都必须将训练数据拆分为K折，进行K次训练和评估。如果我们有10组超参数并且使用5-Fold CV，那就代表了50个训练循环。幸运的是，与机器学习中的大多数问题一样，有人解决了我们的问题，使用K-Fold CV进行模型调整可以在Scikit-Learn中自动实现。# 在Scikit-Learn中使用随机搜索交叉验证
通常，我们只有一个模糊的最佳超参数和最佳方法的想法，缩小搜索范围的最佳方法是为每个超参数评估一系列的值。使用Scikit-Learn的RandomizedSearchCV方法，我们可以定义超参数范围的网格，并从网格中随机抽样，使用每个值组合执行K-Fold CV。
在进入模型调整之前，让我们简要回顾一下，我们正在处理一个监督回归机器学习问题。我们正在尝试使用过去的历史天气数据来预测明天在我们的城市（华盛顿州西雅图）的温度。我们有4.5年的训练数据，1.5年的测试数据，并使用6个不同的特征（变量）来进行预测。（要查看数据准备的完整代码，请参见笔记本。）
让我们快速检查一下这些特征。
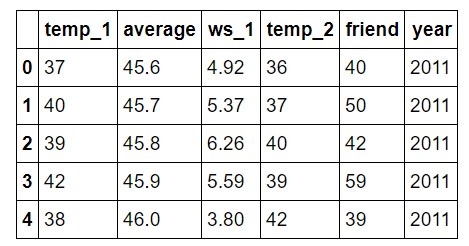
用于温度预测的特征
- temp_1 = 前一天的最高温度（华氏度）
- average = 历史平均最高温度
- ws_1 = 前一天的平均风速
- temp_2 = 两天前的最高温度
- friend = 我们“可靠”的朋友的预测
- year = 日历年份
在之前的文章中，我们检查了数据以查找异常，并且我们知道我们的数据是干净的。因此，我们可以跳过数据清理并直接进入超参数调整。
要查看可用的超参数，我们可以创建一个随机森林并检查默认值。
from sklearn.ensemble import RandomForestRegressorrf = RandomForestRegressor(random_state = 42)from pprint import pprint# Look at parameters used by our current forest
print('Parameters currently in use:\n')
pprint(rf.get_params())Parameters currently in use:
{'bootstrap': True,
'criterion': 'mse',
'max_depth': None,
'max_features': 'auto',
'max_leaf_nodes': None,
'min_impurity_decrease': 0.0,
'min_impurity_split': None,
'min_samples_leaf': 1,
'min_samples_split': 2,
'min_weight_fraction_leaf': 0.0,
'n_estimators': 10,
'n_jobs': 1,
'oob_score': False,
'random_state': 42,
'verbose': 0,
'warm_start': False}
哇，这是一个相当压倒性的列表！我们该从哪里开始呢？一个好的起点是Scikit-Learn中随机森林的文档。这告诉我们最重要的设置是森林中树的数量（n_estimators）和在每个叶节点处考虑用于分割的特征数（max_features）。我们可以阅读随机森林的研究论文并尝试理论化最佳超参数，但更有效地使用我们的时间的方法是尝试一系列不同的值，看看哪个最有效！我们将尝试调整以下一组超参数：
- n_estimators = 森林中的树数
- max_features = 分割节点时考虑的最大特征数
- max_depth = 每个决策树中的最大层数
- min_samples_split = 在节点拆分之前放置在节点中的最小数据点数
- min_samples_leaf = 允许在叶节点中的最小数据点数
- bootstrap = 抽样数据点的方法（有或无替换）
随机超参数网格
要使用RandomizedSearchCV，我们首先需要创建一个参数网格，在拟合期间从中进行抽样：
from sklearn.model_selection import RandomizedSearchCV# Number of trees in random forest
n_estimators = [int(x) for x in np.linspace(start = 200, stop = 2000, num = 10)]
# Number of features to consider at every split
max_features = ['auto', 'sqrt']
# Maximum number of levels in tree
max_depth = [int(x) for x in np.linspace(10, 110, num = 11)]
max_depth.append(None)
# Minimum number of samples required to split a node
min_samples_split = [2, 5, 10]
# Minimum number of samples required at each leaf node
min_samples_leaf = [1, 2, 4]
# Method of selecting samples for training each tree
bootstrap = [True, False]# Create the random grid
random_grid = {'n_estimators': n_estimators,
'max_features': max_features,
'max_depth': max_depth,
'min_samples_split': min_samples_split,
'min_samples_leaf': min_samples_leaf,
'bootstrap': bootstrap}pprint(random_grid){'bootstrap': [True, False],
'max_depth': [10, 20, 30, 40, 50, 60, 70, 80, 90, 100, None],
'max_features': ['auto', 'sqrt'],
'min_samples_leaf': [1, 2, 4],
'min_samples_split': [2, 5, 10],
'n_estimators': [200, 400, 600, 800, 1000, 1200, 1400, 1600, 1800, 2000]}
在每次迭代中，算法将选择不同的特征组合。总共有2 * 12 * 2 * 3 * 3 * 10 = 4320个设置！但是，随机搜索的好处是我们不是尝试每个组合，而是随机选择以对一系列值进行抽样。
随机搜索训练
现在，我们实例化随机搜索并像任何Scikit-Learn模型一样拟合它：
# Use the random grid to search for best hyperparameters
# First create the base model to tune
rf = RandomForestRegressor()
# Random search of parameters, using 3 fold cross validation,
# search across 100 different combinations, and use all available cores
rf_random = RandomizedSearchCV(estimator = rf, param_distributions = random_grid, n_iter = 100, cv = 3, verbose=2, random_state=42, n_jobs = -1)# Fit the random search model
rf_random.fit(train_features, train_labels)
RandomizedSearchCV中最重要的参数是n_iter，它控制要尝试的不同组合的数量，以及cv，它是用于交叉验证的折叠数（我们分别使用100和3）。更多的迭代将涵盖更广泛的搜索空间，更多的cv折叠减少了过度拟合的机会，但提高每个参数会增加运行时间。机器学习是一个权衡的领域，性能与时间之间的权衡是最基本的之一。
我们可以查看拟合随机搜索的最佳参数：
rf_random.best_params_{'bootstrap': True,
'max_depth': 70,
'max_features': 'auto',
'min_samples_leaf': 4,
'min_samples_split': 10,
'n_estimators': 400}
从这些结果中，我们应该能够缩小每个超参数的值范围。
评估随机搜索
为了确定随机搜索是否产生了更好的模型，我们将基准模型与最佳随机搜索模型进行比较。
def evaluate(model, test_features, test_labels):
predictions = model.predict(test_features)
errors = abs(predictions - test_labels)
mape = 100 * np.mean(errors / test_labels)
accuracy = 100 - mape
print('Model Performance')
print('Average Error: {:0.4f} degrees.'.format(np.mean(errors)))
print('Accuracy = {:0.2f}%.'.format(accuracy))
return accuracybase_model = RandomForestRegressor(n_estimators = 10, random_state = 42)
base_model.fit(train_features, train_labels)
base_accuracy = evaluate(base_model, test_features, test_labels)Model Performance
Average Error: 3.9199 degrees.
Accuracy = 93.36%.best_random = rf_random.best_estimator_
random_accuracy = evaluate(best_random, test_features, test_labels)Model Performance
Average Error: 3.7152 degrees.
Accuracy = 93.73%.print('Improvement of {:0.2f}%.'.format( 100 * (random_accuracy - base_accuracy) / base_accuracy))Improvement of 0.40%.
我们取得了0.4％的准确度不太显着的提高。但根据应用程序的不同，这可能是一个显着的优势。我们可以使用网格搜索进一步改进随机搜索中找到的最有前途的超参数范围。
带交叉验证的网格搜索
随机搜索使我们缩小了每个超参数的范围。现在，我们知道在哪里集中我们的搜索，我们可以明确指定要尝试的每个设置组合。我们使用GridSearchCV进行这个方法，该方法评估我们定义的所有组合，而不是从分布中随机抽样。要使用Grid Search，我们基于随机搜索提供的最佳值再创建一个网格：
from sklearn.model_selection import GridSearchCV# Create the parameter grid based on the results of random search
param_grid = {
'bootstrap': [True],
'max_depth': [80, 90, 100, 110],
'max_features': [2, 3],
'min_samples_leaf': [3, 4, 5],
'min_samples_split': [8, 10, 12],
'n_estimators': [100, 200, 300, 1000]
}# Create a based model
rf = RandomForestRegressor()# Instantiate the grid search model
grid_search = GridSearchCV(estimator = rf, param_grid = param_grid,
cv = 3, n_jobs = -1, verbose = 2)
这将尝试1 * 4 * 2 * 3 * 3 * 4 = 288个设置组合。我们可以拟合模型，显示最佳超参数，并评估性能：
# Fit the grid search to the data
grid_search.fit(train_features, train_labels)grid_search.best_params_{'bootstrap': True,
'max_depth': 80,
'max_features': 3,
'min_samples_leaf': 5,
'min_samples_split': 12,
'n_estimators': 100}best_grid = grid_search.best_estimator_
grid_accuracy = evaluate(best_grid, test_features, test_labels)Model Performance
Average Error: 3.6561 degrees.
Accuracy = 93.83%.print('Improvement of {:0.2f}%.'.format( 100 * (grid_accuracy - base_accuracy) / base_accuracy))Improvement of 0.50%.
看起来我们已经达到了最大的性能，但我们可以使用更进一步的网格进行尝试，该网格是从之前的结果进一步精细化的。代码与之前相同，只是使用了不同的网格，因此我只呈现结果：
Model Performance
Average Error: 3.6602 degrees.
Accuracy = 93.82%.Improvement of 0.49%.
性能的小幅下降表明我们已经达到了超参数调整的收益递减。我们可以继续，但最多只能获得微不足道的回报。
比较
我们可以快速比较用于提高性能的不同方法，并显示每种方法的回报。下表显示了我们进行的所有改进的最终结果（包括第一部分的结果）：
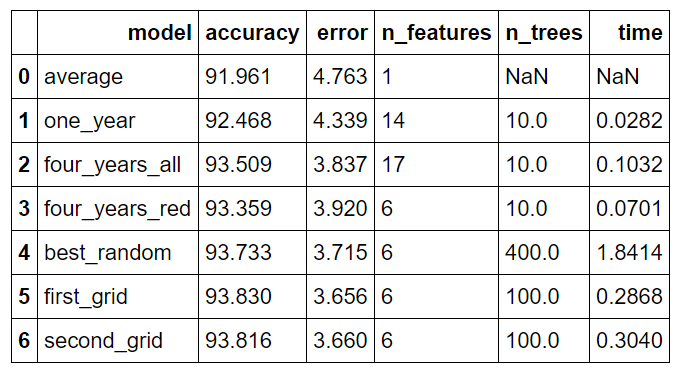所有模型的比较
Model 是模型的名称，accuracy 是百分比准确率，error 是平均绝对误差（以度为单位），n_features 是数据集中的特征数量，n_trees 是森林中的决策树数量，time 是训练和预测所需的时间（以秒为单位）。
模型如下：
- average：通过预测测试集中每天的历史平均最高温度计算的原始基线
- one_year：使用一年的数据训练的模型
- four_years_all：使用 4.5 年的数据和扩展特征训练的模型（详见第一部分）
- four_years_red：使用 4.5 年的数据和最重要特征的子集训练的模型
- best_random：使用交叉验证的随机搜索得到的最佳模型
- first_grid：使用交叉验证的第一次网格搜索得到的最佳模型（选定为最终模型）
- second_grid：使用交叉验证的第二次网格搜索得到的最佳模型
总体而言，收集更多数据和特征选择将误差降低了 17.69%，而超参数进一步将误差降低了 6.73%。
模型比较（详见 Notebook 中的代码）
以程序员小时计算，收集数据大约需要 6 小时，而超参数调整需要大约 3 小时。与生活中的任何追求一样，追求更进一步的优化有时候并不值得，知道何时停止可能与坚持不懈一样重要（很抱歉让你们陷入哲学思考）。此外，在任何数据问题中，都存在所谓的 Bayes error rate，即问题中可能的最小绝对误差。Bayes 错误率，也称为可重现误差，是潜在变量和任何物理过程固有噪声的组合，这些因素都是我们无法测量的。因此，创建完美的模型是不可能的。尽管如此，在这个例子中，我们通过超参数调整能够显著改善模型，并且涵盖了许多广泛适用的机器学习主题。
训练可视化
为了进一步分析超参数优化过程，我们可以逐个更改设置，查看对模型性能的影响（本质上进行受控实验）。例如，我们可以创建一个包含一系列树数量的网格，执行网格搜索 CV，然后绘制结果。绘制训练和测试误差以及训练时间将使我们能够检查更改一个超参数对模型的影响。
首先，我们可以查看更改森林中树的数量的影响。（详见 notebook 中的训练和绘图代码）
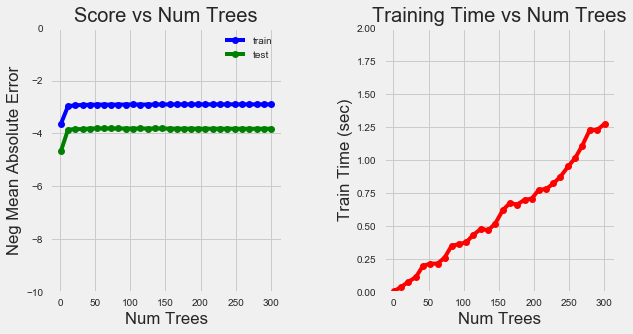
树的数量训练曲线
随着树的数量增加，误差减少，但是到了一定程度后，增加树的数量对准确性的提升并不明显（我们的最终模型有 100 棵树），而训练时间则持续上升。
我们还可以查看分裂节点的特征数的曲线：
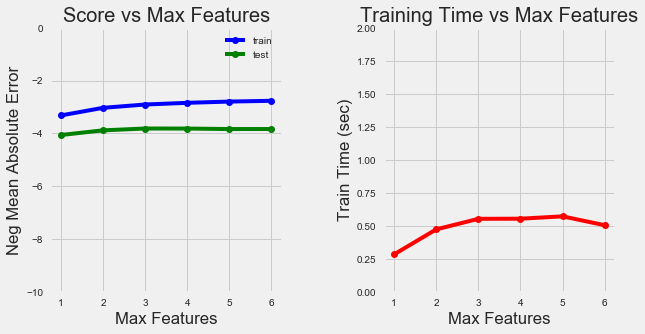
特征数量训练曲线
随着保留的特征数量增加，模型准确性如预期般增加。训练时间也会增加，但不会显著增加。
结合定量统计数据，这些可视化内容可以让我们了解不同超参数组合之间的权衡。虽然通常无法预先知道哪些设置最有效，但是本例演示了 Python 中的简单工具，可以让我们优化机器学习模型。
如往常一样，我欢迎反馈和建设性批评。我的邮箱是 wjk68@case.edu。
评论(0)