k-最近邻(KNN)算法是一种简单易用的有监督机器学习算法,可用于解决分类和回归问题。先停一下!我们来详细解释一下。

ABC,我们保持超级简单!
分解
一个有监督的机器学习算法(与无监督机器学习算法相对)是指依赖于标记的输入数据来学习一个函数,以便在给定新的未标记数据时产生适当的输出。
想象一下计算机是一个孩子,我们是它的监督员(例如父母、监护人或老师),我们希望这个孩子(计算机)学会什么是猪。我们会向孩子展示几张不同的图片,其中一些是猪,其余可能是任何东西(猫、狗等)。
当我们看到一只猪时,我们大喊“猪!”当不是猪时,我们大喊“不是猪!”在与孩子多次进行此操作后,我们向他们展示一张图片并问“猪?”他们会正确(大多数情况下)地说“猪!”或“不是猪!”这就是有监督机器学习。

“猪!”
有监督机器学习算法用于解决分类或回归问题。
一个分类问题的输出是一个离散值。例如,“喜欢菠萝披萨”和“不喜欢菠萝披萨”是离散的。没有中间地带。上面教孩子识别猪的类比是分类问题的另一个例子。

显示随机生成的数据的图像
这张图片展示了分类数据可能看起来像什么的基本例子。我们有一个预测器(或一组预测器)和一个标签。在图片中,我们可能会尝试根据年龄(预测器)预测某个人是否喜欢在披萨上加菠萝(1)或不喜欢(0)。
通常,将分类算法的输出(标签)表示为整数,例如1、-1或0是标准做法。在这种情况下,这些数字纯粹是代表性的。不应对它们执行数学运算,因为这样做是没有意义的。想一想,什么是“喜欢菠萝”+“不喜欢菠萝”?恰恰是这样。我们不能将它们加在一起,因此我们不应该添加它们的数字表示。
一个回归问题的输出是一个实数(带小数点的数字)。例如,我们可以使用下表中的数据估计某人的体重,给定他们的身高。
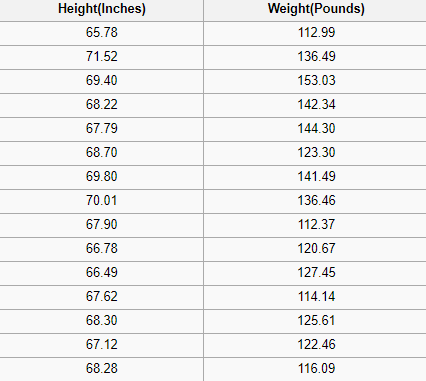
显示一部分 SOCR身高和体重数据集
在回归分析中使用的数据看起来与上面的图像中显示的数据类似。我们有一个独立变量(或一组独立变量)和一个依赖变量(我们试图在给定独立变量的情况下猜测的东西)。例如,我们可以说身高是独立变量,体重是依赖变量。
此外,每一行通常称为示例、观察或数据点,而每一列(不包括标签/依赖变量)通常称为预测器、维度、独立变量或特征。
一个无监督机器学习算法利用没有任何标签的输入数据,也就是没有老师(标签)告诉孩子(计算机)何时是正确的,何时犯了错误,以便它可以自我纠正。
与试图学习一个函数以允许我们根据一些新的未标记数据进行预测的有监督学习不同,无监督学习试图学习数据的基本结构,以便为我们提供更多关于数据的见解。
K-最近邻
KNN算法假设相似的东西在紧密的邻近存在。换句话说,相似的东西彼此接近。
“物以类聚,人以群分。”
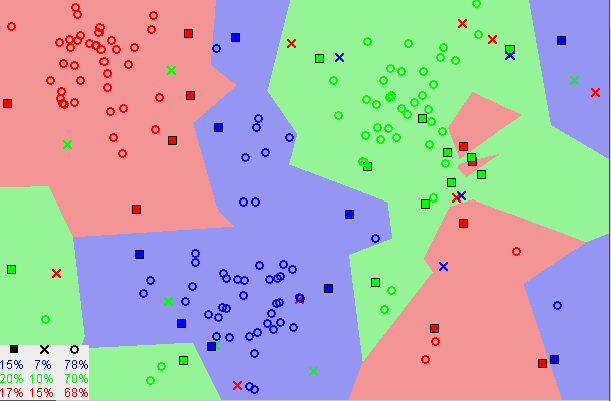
请注意,上面的图像中大多数时候,相似的数据点是靠近彼此的。KNN算法依赖于这种假设足够真实,以便算法有用。KNN使用我们可能在童年时学过的一些数学来捕捉相似性(有时称为距离、接近度或亲近度)-计算图上点之间的距离。
注意: 在继续之前,需要了解如何计算图上点之间的距离。如果你不熟悉或需要刷新一下如何进行此计算,请彻底阅读“2点之间的距离”,然后立即回来。
有其他计算距离的方法,根据我们解决的问题,可能有一种方法更可取。然而,直线距离(也称为欧几里德距离)是一个流行且熟悉的选择。
KNN算法
- 加载数据
- 初始化K为你选择的邻居数
- 对于数据中的每个示例
3.1 计算查询示例和数据中当前示例之间的距离。
3.2 将距离和示例的索引添加到有序集合中
-
按距离从小到大(升序)排序距离和索引的有序集合
-
从排序的集合中选择前K个条目6. 获取选择的K个条目的标签
-
如果是回归问题,返回K个标签的平均值
-
如果是分类问题,返回K个标签的众数
从头实现KNN算法
选择合适的K值
为了选择适合你的数据的K值,我们需要使用不同的K值多次运行KNN算法,并选择在减少错误的同时保持算法在给定未见过数据时准确预测的能力的K值。
以下是需要记住的一些事情:
- 当我们将K值降低到1时,我们的预测变得不太稳定。想一想,假设K=1,我们有一个查询点,周围有几个红色和一个绿色(我在想彩色图中左上角),但绿色是单个最近的邻居。理性地说,我们认为查询点最有可能是红色的,但由于K=1,KNN错误地预测查询点是绿色的。
- 相反,当我们增加K的值时,我们的预测变得更加稳定,因为通过多数投票/平均,预测更有可能做出更准确的预测(在一定程度上)。最终,我们开始看到错误数量增加。此时我们知道我们已经将K值推得太远了。
- 在进行多数投票(例如,在分类问题中选择众数)的情况下,我们通常将K设为奇数以进行决胜投票。
优点
- 该算法简单易用。
- 不需要构建模型、调整多个参数或进行其他假设。
- 该算法具有通用性。它可用于分类、回归和搜索(如下一节所示)。
缺点
- 当示例数量和/或预测变量/自变量数量增加时,算法的速度显著降低。
实践中的KNN
KNN的主要缺点是随着数据量的增加而显著变慢,使其在需要快速进行预测的环境中成为一个不切实际的选择。此外,还有更快速的算法可以产生更准确的分类和回归结果。
但是,如果你有足够的计算资源来快速处理用于预测的数据,KNN仍然可以用于解决需要识别相似对象的问题。一个例子是在推荐系统中使用KNN算法,这是KNN搜索的一种应用。
推荐系统
在大规模情况下,这将像在亚马逊上推荐产品,在Medium上推荐文章,在Netflix上推荐电影或在YouTube上推荐视频。尽管我们可以肯定地说,它们都使用更有效的方法进行推荐,因为它们处理的数据量非常庞大。
但是,我们可以使用本文中所学到的知识在较小的规模上复制其中一个推荐系统。让我们构建一个电影推荐系统的核心。
我们要回答的问题是什么?
给定我们的电影数据集,与电影查询最相似的5部电影是什么?
收集电影数据
如果我们在Netflix、Hulu或IMDb工作,我们可以从他们的数据仓库中获取数据。由于我们没有在这些公司工作,我们必须通过其他方式获取数据。我们可以使用UCI机器学习库、IMDb的数据集或费力地创建自己的数据集来使用一些电影数据。
探索、清理和准备数据
无论我们从哪里获取数据,可能存在一些问题需要我们在将其传送到KNN算法之前进行纠正,以准备好数据。例如,数据可能不符合算法期望的格式,或者可能存在需要填充或删除的缺失值。
我们上面的KNN实现依赖于结构化数据。它需要在表格格式中。此外,该实现假定所有列都包含数值数据,并且我们数据的最后一列具有我们可以执行某些函数的标签。因此,无论我们从哪里获取数据,都需要使其符合这些约束条件。
下面的数据是我们清理后的数据的示例。该数据包含30部电影,包括每部电影在七种流派和它们的IMDB评级中的数据。标签列全部为零,因为我们不使用此数据集进行分类或回归。
自制电影推荐数据集
此外,当使用KNN算法时,将不考虑电影之间的关系(例如演员、导演和主题),因为捕获这些关系的数据在数据集中丢失。因此,当我们在数据上运行KNN算法时,相似性将仅基于包含的流派和电影的IMDB评级。
使用算法
想象一下。我们正在浏览MoviesXb网站,这是一个虚构的IMDb衍生网站,我们遇到了《潘多拉之盒》。我们不确定是否想观看它,但它的流派引起了我们的兴趣;我们对其他类似的电影很好奇。我们向下滚动到“更多类似内容”部分,看看MoviesXb将做出什么推荐,算法的齿轮开始转动。
MoviesXb网站向其后端发送请求,以获取与《潘多拉之盒》最相似的5部电影。后端具有与我们完全相同的推荐数据集。它首先为《潘多拉之盒》创建行表示(更好地称为特征向量),然后运行类似于下面程序的程序来搜索与《潘多拉之盒》最相似的5部电影,并最终将结果发送回MoviesXb网站。
当我们运行此程序时,我们可以看到MoviesXb推荐《为奴十二年》、《血战钢锯岭》、《卡特女王》、《风之谷》和《美丽心灵》。现在我们完全理解了KNN算法的工作原理,能够准确地解释KNN算法如何做出这些推荐。祝贺你!
总结
k最近邻(KNN)算法是一种简单的监督式机器学习算法,可用于解决分类和回归问题。它易于实现和理解,但有一个主要缺点,随着使用数据的大小增加,速度会显著变慢。
KNN的工作方式是找到查询点与数据中所有示例之间的距离,选择与查询点最接近的指定数量的示例(K),然后投票选择最频繁的标签(在分类问题中)或平均标签(在回归问题中)。在分类和回归的情况下,我们看到选择适合数据的正确K是通过尝试几个K并选择最佳的一个来完成的。
最后,我们看了一个例子,展示了KNN算法如何用于推荐系统,这是KNN搜索的一种应用。

KNN如此说道……“告诉我你的朋友,我就能知道你是谁。”
补充说明
[1] 本文中实现的KNN电影推荐器对于电影查询可能是推荐数据集的情况没有进行处理,这是为了简单起见。在生产系统中可能是不合理的,应该进行适当处理。











评论(0)