时间序列预测是一个难题，没有简单的答案。有无数的统计模型声称在效果上优于其他模型，但往往并不清楚哪个模型最好。

话虽如此，基于ARMA的模型通常是一个很好的起点模型。它们可以在大多数时间序列问题上获得不错的得分，并且适合作为任何时间序列问题的基准模型。

本文是一篇全面、适合初学者的指南，旨在帮助你理解基于ARIMA的模型。

简介

ARIMA模型缩写代表“自回归积分移动平均”，在本文中，我们将其分解为AR、I和MA。

自回归部分-AR(p)

ARIMA模型的自回归部分由AR(p)表示，其中p参数确定我们使用的滞后序列的数量。

AR公式-作者提供

AR(0)：白噪声

如果我们将p参数设置为零（AR(0)），即没有自回归项。这个时间序列只是白噪声。每个数据点从均值为0、方差为sigma-squared的分布中采样。这导致了一系列无法预测的随机数。这真的很有用，因为它可以作为零假设，并保护我们的分析不接受错误的正面模式。

AR(1)：随机游走和振荡

当将p参数设置为1时，我们考虑前一个时间戳通过乘数调整后的值，然后加上白噪声。如果乘数为0，我们得到白噪声，如果乘数为1，我们得到一个随机游走。如果乘数在0 < α₁ < 1之间，则时间序列将表现出均值回归。这意味着值倾向于围绕0徘徊，并在从其回归后回归均值。

AR(p)：高阶项

将p参数进一步增加只意味着进一步回溯并添加更多时间戳，这些时间戳由它们自己的乘数调整。我们可以回溯到任何程度，但随着我们越往后，越有可能我们应该使用其他参数，例如移动平均（MA(q)）。

移动平均-MA(q)

“这个组件不是滚动平均，而是白噪声中的滞后。” - Matt Sosna

MA(q)

MA(q)是移动平均模型，q是预测中滞后的预测误差项的数量。在MA(1)模型中，我们的预测是一个常数项加上上一个白噪声项乘以一个乘数，加上当前白噪声项。这只是简单的概率+统计，因为我们根据以前的白噪声项调整我们的预测。

ARMA和ARIMA模型

ARMA和ARIMA架构只是将AR（自回归）和MA（移动平均）组件放在一起。

ARMA

ARMA模型是一个常数加上AR滞后和它们的乘数的总和，加上MA滞后和它们的乘数的总和加上白噪声。这个方程是所有接下来的模型的基础，是跨不同领域的许多预测模型的框架。

ARIMA

_ARIMA模型是一个ARMA模型，但在模型中包括一个预处理步骤，我们使用I(d)来表示。I(d)是差分阶数，即需要进行转换使数据平稳的转换数量。因此，ARIMA模型只是差分时间序列上的ARMA模型。

SARIMA、ARIMAX、SARIMAX模型

ARIMA模型很棒，但在模型中包括季节性和外生变量可能非常强大。由于ARIMA模型假设时间序列是平稳的，我们需要使用不同的模型。

SARIMA

进入SARIMA（季节性ARIMA）。这个模型与ARIMA模型非常相似，只是增加了一组额外的自回归和移动平均分量。附加的滞后与季节性频率偏移（例如12-月度，24-每小时）。

SARIMA模型允许通过季节性频率和非季节性差分对数据进行差分。通过自动参数搜索框架（例如pmdarina），可以更轻松地确定哪些参数最好。

ARIMAX和SARIMAX

上面是SARIMAX模型的公式。该模型考虑外生变量，或者换句话说，使用外部数据进行预测。外生变量的一些现实世界的例子包括黄金价格、石油价格、室外温度、汇率。

有趣的是，所有外生因素在历史模型预测中仍然被间接地建模。话虽如此，如果我们包括外部数据，模型将比依赖滞后项的影响更快地响应其影响。

代码示例

让我们通过Python中的一个简单代码示例来了解这些模型。

加载数据

对于此示例，我们将使用空中乘客数据集。此数据集包含从1949年初到1960年底的空中旅行乘客数量。

该数据集具有正趋势和年度季节性。

一旦读取数据集，索引将设置为日期。这是在Pandas中处理时间序列数据的标准做法，并使得实现ARIMA、SARIMA和SARIMAX更容易。

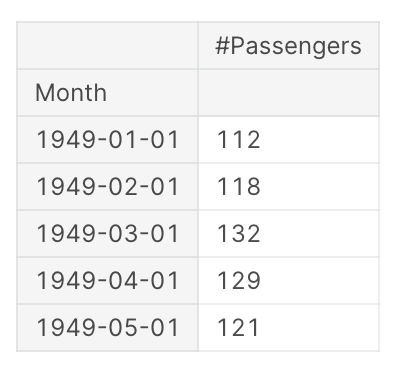
单元输出 — 作者提供

趋势

数据随时间的总体方向。例如，如果我们观察一个新生婴儿的身高，他们的身高会随着时间逐渐增长。另一方面，一个成功的减肥计划中，人们的体重会随时间逐渐下降。

季节性+循环

任何具有固定频率的季节性或重复模式。可以是每小时、每月、每天、每年等。其中一个例子是冬季外套的销售在冬季月份增加，在夏季月份减少。另一个例子是你的银行账户余额。在每个月的前10天，你的余额会随着你支付月租、水电费和其他账单支付而下降。

不规则+噪声

数据中任何大的峰值或低谷。其中一个例子是你跑400米赛跑时的心率。当你开始比赛时，你的心率与你一天中的心率相似，但在比赛中，它会在短时间内急剧上升到更高的水平，然后返回到正常水平。

在下面的航空旅客数据可视化中，我们可以查看这些组成部分。乍一看，数据似乎有一个正向趋势和某种季节性或周期性。数据中似乎没有任何重大的不规则或噪声。

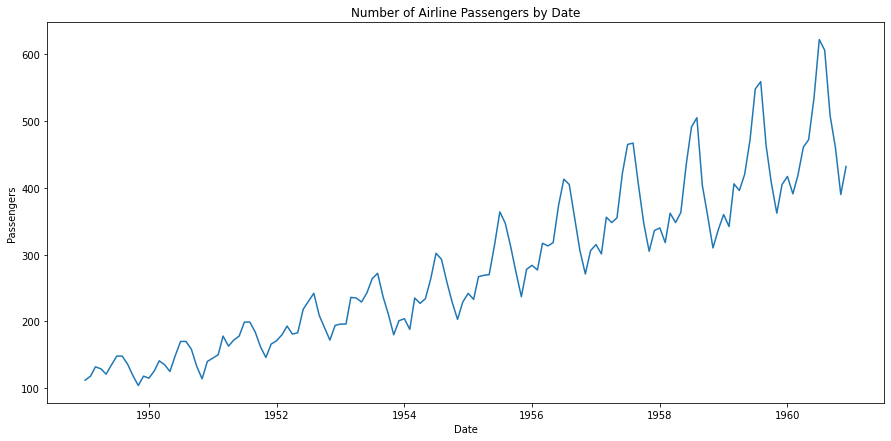
航空旅客线图 — 作者提供

滚动统计

滚动平均值是可视化数据趋势的好方法。由于数据集提供按月计数，窗口大小为12将为我们提供年度滚动平均值。

我们还将包括滚动标准差，以了解数据与滚动平均值的偏差程度。

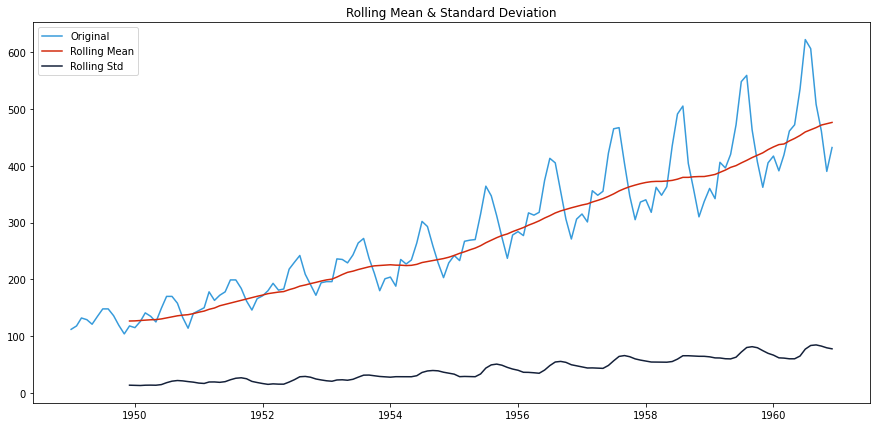
滚动统计图 — 作者提供

增广迪基-富勒测试

增广迪基-富勒测试用于确定时间序列数据是否为平稳数据。类似于t检验，我们在测试之前设置一个显著性水平，并根据结果p值得出假设的结论。

零假设： 数据不是平稳的。

备择假设： 数据是平稳的。

对于数据来是平稳的（即拒绝零假设），ADF测试应该具有：

• p值 <= 显著性水平（0.01、0.05、0.10等）

如果p值大于显著性水平，则我们可以说数据很可能不是平稳的。

我们可以看到下面的ADF测试中，p值为0.991880，这意味着数据很可能不是平稳的。

ADF测试输出 — 作者提供

ARIMA模型选择w/ Auto-ARIMA

虽然我们的数据几乎肯定不是平稳的（p值=0.991），但让我们看看标准ARIMA模型在时间序列上的表现如何。

使用pmdarima包中的auto_arima()函数，我们可以对模型的最佳值进行参数搜索。

模型诊断

plot_diagnostics函数会生成四个图形。标准化残差、直方图加KDE估计、正态Q-Q和自相关图。

我们可以根据以下条件解释模型是否拟合良好。

标准化残差

残差中没有明显的模式，其值的平均值为零，方差均匀。

直方图加KDE估计

KDE曲线应该与正态分布非常相似（在图中标记为N(0,1)）

正态Q-Q

大多数数据点应该位于直线上

自相关图(ACF图)

大于零滞后的95%相关性不应显着。灰色区域是置信区间，如果值落在此区间之外，则它们在统计上是显着的。在我们的情况下，有一些值在此区域之外，因此我们可能需要添加更多的预测变量以使模型更准确。

Arima诊断图 — 作者提供

然后，我们可以使用模型来预测未来24个月的航空旅客数量。

正如下面的图表所示，这似乎不是非常准确的预测。也许我们需要改变模型结构，以便考虑季节性？

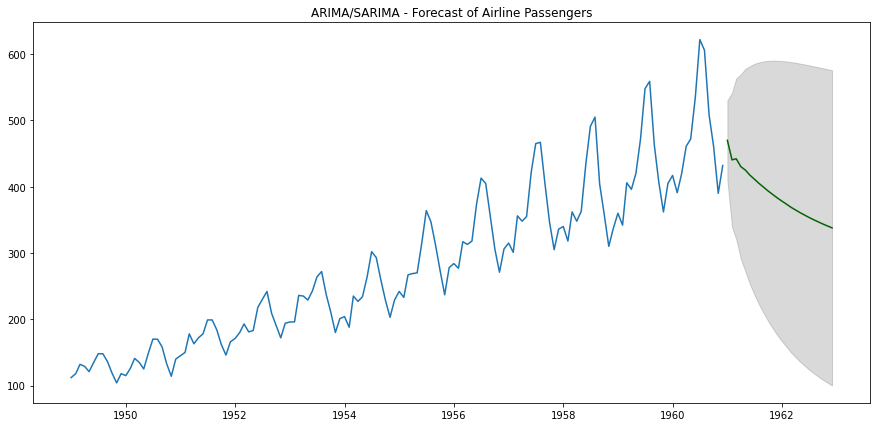
ARIMA预测 — 作者提供

SARIMA模型

现在让我们尝试与上面相同的策略，只是我们使用SARIMA模型，以便考虑季节性。

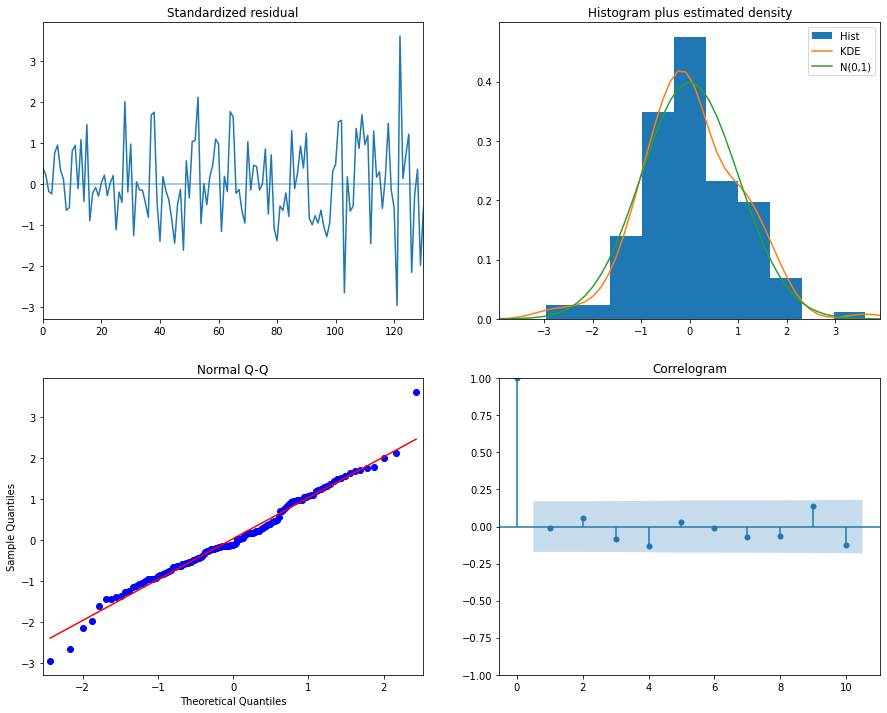
查看模型诊断时，与标准ARIMA模型相比，我们可以看到一些显着差异。

标准化残差

标准化残差在整个图中更加一致，这意味着数据更接近平稳。

直方图加KDE估计

KDE曲线与正态分布相似（这里没有太多变化）。

正态Q-Q

数据点比ARIMA诊断图中更接近直线。

自相关图(ACF图)

灰色区域是置信区间，如果值落在此区间之外，则它们在统计上是显着的。我们希望所有值都在此区域内。添加季节性组件可以实现这一点！现在所有点都在95%置信区间内。

``` SARIMA诊断

我们可以像之前一样，使用模型来预测未来24个月的航空公司乘客人数。

如下图所示，这似乎比标准ARIMA模型更准确！

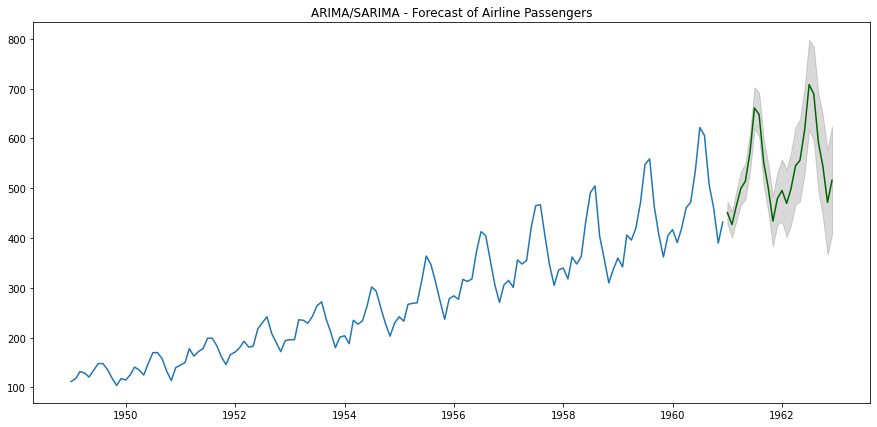
SARIMA预测 - 作者提供

SARIMAX模型选择

现在让我们练习添加外生变量。在这个例子中，我只是简单地将月份作为外生变量添加进去，但这并不是特别有用，因为这已经通过季节性传达出来了。

请注意，我们在传递给SARIMAX模型的数据周围添加了额外的方括号。

从以下预测中，我们可以看到我们得到了一些相当不错的预测，预测的置信区间宽度已经减小。这意味着模型对其预测更加确定。

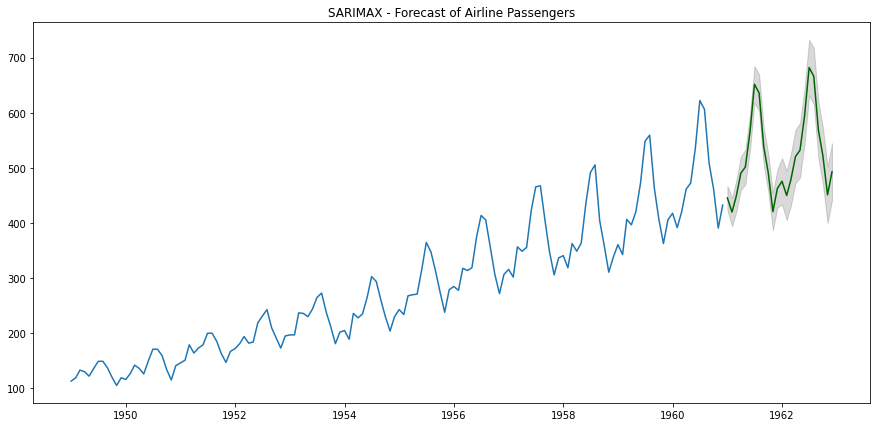
SARIMAX预测 - 作者提供

总结

请在这里找到本文的代码。

用自己的话来表达思想并实现ARIMA模型是学习的最佳方式。希望本文能激励其他人也这样做。

ARIMA模型架构提供比RNN更多的可解释性，但RNN被认为能生成更准确的预测。现在我对ARIMA模型架构有了很好的理解，我需要研究LSTM和RNN深度学习模型来预测时间序列数据！

译自：https://towardsdatascience.com/time-series-forecasting-with-arima-sarima-and-sarimax-ee61099e78f6